This article will be a brief overview of how to implement a simple animation compression scheme and some of the concepts associated with it. I am by no means an expert in the topic but there’s very little information on the topic and the information out there is relatively fragmented. If you would like to read more in depth articles on the topic, the following links are a great read and contain a lot of in-depth information:
- https://nfrechette.github.io/2016/10/21/anim_compression_toc/
- https://technology.riotgames.com/news/compressing-skeletal-animation-data
- http://bitsquid.blogspot.com/2009/11/bitsquid-low-level-animation-system.html
- http://bitsquid.blogspot.com/2011/10/low-level-animation-part-2.html
So before we get started it’s worth doing a quick intro to skeletal animation and some of the basic concepts.
Animation and Compression Basics
Skeletal animation is a relative simple topic if you ignore skinning. We have the concept of a skeleton which contains the bone transforms for a character. These bone transforms are kept in a hierarchical format, basically each bone is stored as the delta between its global position and it’s parent. Terminology here gets confusing since in a game engine, often local refers to model/character space, and global refers to world space. In terms of animation local means bone parent space, and global can mean either character space or world space depending if you have root motion but lets not worry too much about that. The important part is that bone transforms are stored local to their parents. This has numerous benefits primarily in terms of blending. when we blend two poses if the bones were global they would linearly interpolate in position, which will cause limbs to grow and shrink thereby deforming the character. If you use deltas, when you blend you simply blend from one difference to another so if the translation delta is the same between two poses for a given bone the bone’s length will stay constant. I think the simplest (not 100% correct) way to think of it is that using delta will result in “spherical” movement of bone positions during the blend whereas blending the global transforms will result in linear movement of the bones positions.
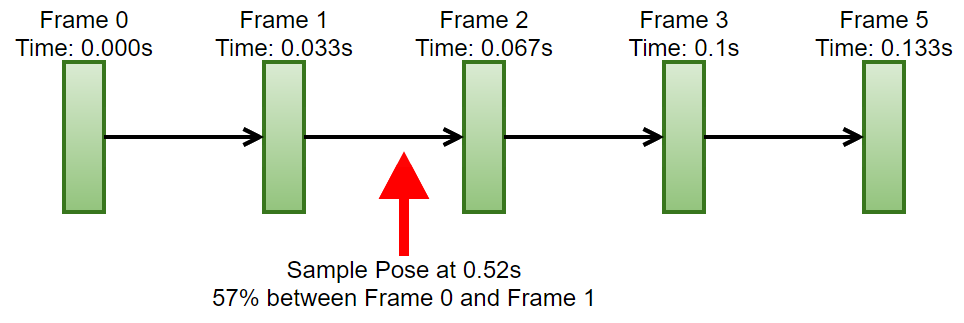
A skeletal animation is simply a sequential list of keyframes at a (usually) fixed framerate. A keyframe is a skeletal pose. When you want to get a pose that lies in between keyframes, you would sample both keyframes and blend between them using the fractional time between them as the blend weight. If we look at the example below, we have an animation that’s authored at 30fps. The animation has a total of 5 frames and we’ve been asked to get the pose at time 0.52s from the start. So we need to sample the pose at frame 1 and the pose at frame 2 and blend between them with a blend weight of ~57%.
Given the above information and assuming memory is not an issue the ideal way to store an animation would be to store the pose sequentially, as show below:

Why is this ideal? Well, sampling a given keyframe is reduced to a simple memcpy operation. And sampling an intermediate pose is two memcpy’s and a blend operation. In terms of cache, you are memcpy’ing two sequential blocks of data, so once you copy the first frame, you already have the second frame in one of your caches. Now you might also say, hold on, when we blend, we have to blend all the bones, what if a large number of them didn’t change frame to frame, isn’t it better to just store the bones as tracks and then only blend the transforms that changed… Well, to do that you will incur potentially a few more cache misses jumping around to read individual tracks and then you’d need to check which transforms need blending and so on… The blend might seem like a lot of work but it’s the same instruction on two blocks of memory already in the cache. Your blending code is also relatively simple, often just a set of SIMD instructions with no branching, a modern processor will chew through that in no time.
Now the problem with this approach is that it’s extremely wasteful of memory especially in games where the following is true of 95% of our data.
- Bones are constant length
- Characters in most games don’t stretch their bones so in a given animation most of the translation tracks are constant.
- We dont usually scale bones
- Scale is something that is rarely used in game animation. It’s quite common in film and VFX but not so much in games. Even when it’s used, we pretty much only use uniform scale.
- In fact, for most of the animation runtimes I’ve built I make use of this fact to store an entire bone transform in 8 floats. 4 for the quaternion rotation, 3 for the translation and 1 for the scale. This reduces the runtime pose size considerably, offering performance benefits in terms of blending and copying.
Given this information, when we look at the original data format, we can see that we are extremely wasteful in terms of memory. We duplicate every single bone’s translation and scale values even though they dont change. This quickly gets out of hand. Animators usually author animations at 30fps, and in AAA we have around 100 bones in an average character. So given that info and the 8 float format above, we end up needing ~3KB per pose and ~94KB per second of animation. This quickly adds up and we can easily bust the memory budgets on some platforms.
So let’s talk compression, when trying to compress anything you have to consider several things:
- Compression Ratio
- How much did you manage to reduce the memory
- Quality
- How much information did we lose from the original data
- Compression Performance
- How long does it take to compress the data
- Decompression Performance
- How slow is it to decompress and read the data compared to the uncompressed data.
In my case, I am extremely concerned about quality and performance and less so about memory. I am also working in game animation and so I can leverage the fact that we dont really use translation and scale in our data to help with the memory aspects and so avoid having to lose quality through frame reduction and other lossy approaches.
It’s also super important to note that you shouldn’t underestimate the performance implications of animation compression, on one past project, we integrated a new animation compression scheme from another team and ended up with a ~35% reduction in sampling performance in addition to some quality problems.
So how do we go about compressing animation data, well there are two main areas to look into:
- How can we compress individual pieces of information in a keyframe (quaternions, floats, etc…).
- How can we compress the sequence of keyframes to remove redundant information.
Data Quantization
Pretty much this entire section can be reduced to: quantize your data…
Quantization is a fancy way of saying that you want to convert a value from a continuous range to a discrete set of values.
Float Quantization
When it comes to float quantization, we are trying to take a float value, and represent it as an integer using less bits. The trick is what that integer represents, it doesnt actually represent the original number, instead it represents a value in a discrete range that is mapped to a continuous range. We generally use a very simple approach to this. To quantize a value we first need a range for the original value, once we have this range we normalize the original value over that range. This normalized value is then multiplied by the maximum value possible for the given output bit size we want. So for a 16 bits, we would multiply by 65535. The resulting value is then rounded to the nearest integer and stored. This is shown visually below:
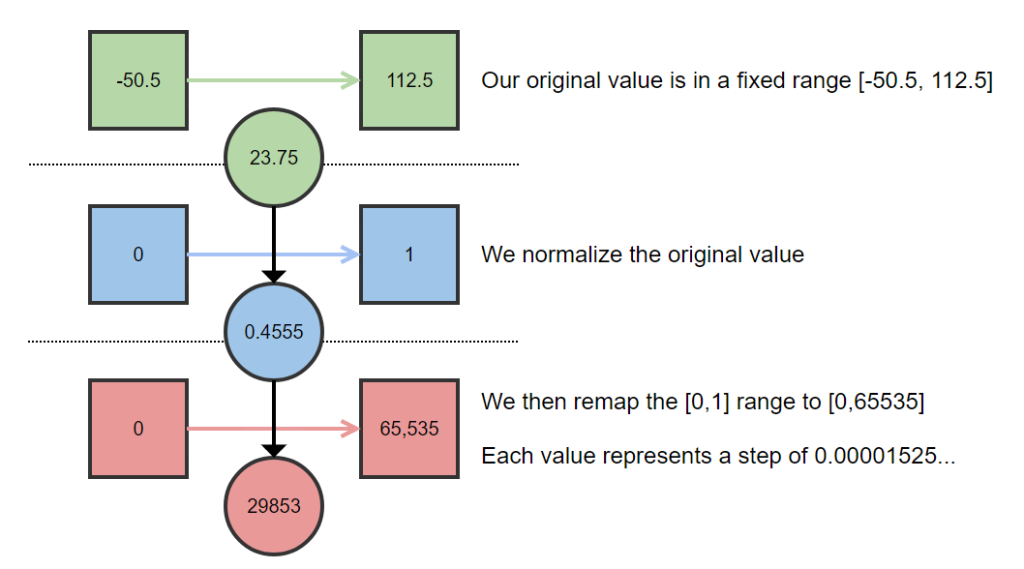
To get back the original value, we simply perform the operations in reverse. What’s important to note here is that we need to record the original range of the value somewhere or we cannot decode the quantized value. The number of bits in the quantized value define the step size in the normalized range and thereby the step size in the original range, given the decoded value will end up on a multiple of the step size, this gives you an easy way to calculate the maximum error you can introduce through the quantization process and so you can decide on the number of bits relevant to your application.
I’m not going to provide any source code examples since there’s a quite nice and simple library for doing basic quantization and is a great reference for the topic: https://github.com/r-lyeh-archived/quant (I will say that you probably dont want to use their quaternion quantization function but more on that later).
Quaternion Compression
Quaternion compression is a relatively well discussed topic so I’m not going to repeat things that other have explained better. Here’s a link to a post on snapshot compression that provides best writeup on the topic: https://gafferongames.com/post/snapshot_compression/
I will say one thing on the topic though. In the bitsquid blog posts, when they talk about quaternion compression they suggest that you compress a quaternion down to 32 bits using around 10 bits of data per quaternion component. This is exactly what the Quant library does as it is based on the bitsquid blog post. This is too much compression in my opinion and caused a lot of shaking in my tests. Perhaps they had shallower character hierarchies, but when multiplying out 15+ of those quaternions in my example animations, the compound error becomes quite severe. 48bits per quaternion in my opinion is the ABSOLUTE minimum precision you can get away with.
Size Reduction from Quantization
So before we discuss the various ways of compressing and laying out our tracks, lets see what sort of compression we’ll get if we just use quantization in our original layout. We’ll use the same example as before (100 bone skeleton) so if we use 48bits (3x16bit) for a quaternion and 48bits (3×16) for the translation and 16bits for the scale, we need a total of 14bytes for a bone transform instead of 32bytes. That’s 43.75% of the original size. So for a 1s animation at 30FPS, we’ve gone from ~94KB to ~41KB.
That’s not too bad, quantization is a relatively cheap operation so our decompression times are not too badly affected either. This is a decent starting point and in some cases, this might even be enough to get your animations within budget and still provide excellent quality and performance.
Track Compression
This is where things can get really complicated especially once people start trying to do things like key reduction, curve fitting, etc… This is also where you really start to screw up the quality of your animations.
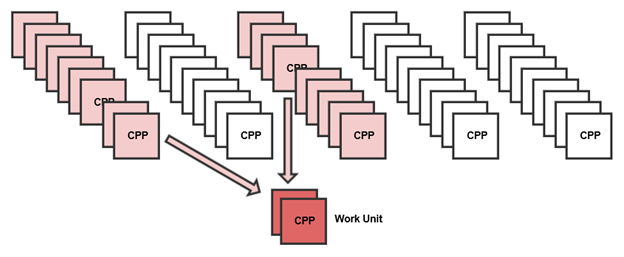
Almost all of these approach assume that each bone’s features (rotation, translation and scale) are stored in an individual track. So we would invert the layout that I had show earlier as follows:

Here we simply store all tracks sequentially but we could also group all rotation, translation and scale tracks together. The basic idea is that we’ve gone from per pose storage to a track based storage.
Once we’ve done this we can do several things to further reduce memory. The first being to start dropping frames. Note: this doesnt require the track format and could be done in the previous layout as well. While this works, it will result in you losing all the subtle movements in the animation as you are throwing away a lot of your data. On PS3, this was heavily used and we would something go down to insane sampling rates like 7 frames per second, usually only for low impact animations. As an animation programmer doing this just leaves a bad taste in my mouth since I can see the lost detail/artistry but if you are coming from a system programmer perspective what you see is that the animation is “mostly” the same as overall movement is still there but you saved a ton of memory…
Let’s ignore that approach as it’s too destructive in my opinion and see what other options we have. Another popular approach is to create a curve for each track and perform key reduction on the curve i.e. remove duplicate keys. n terms of game animation, translation and scale tracks will compress greatly using this approach often reducing down to a single key. This is non-destructive but comes at a decompression cost as you need to evaluate a curve each time you want to get a transform for a given time since you can no longer just jump directly to the data in memory. It can be slightly ameliorated if you only evaluate animations in a single direction and store state for each animation sampler per bone (i.e. where to resume the curve evaluation from) but comes at a increased runtime memory cost and a significant increase to code complexity. Now in modern animation systems, we pretty much dont just play animations from start to finish. We often transition to new animations at specific time offsets due to things like synchronized blending or phase-matching. We often sample specific but not sequential poses from an animation terms to do things like aim/lookat blends and we often play animations backwards. So I wouldn’t recommend trying to do this, it’s just not worth the complexity and potential bugs.
There is also the concept of not just removing identical keys in the curves but specifying a threshold at which similar keys are removed, this results in the animation having a washed out look similar to that when dropping frames as the end result is the same in terms of data. Often you’d see animation compression schemes with per track compression settings and animators constantly screwing with the values trying to keep quality while reducing the size. It’s a painful and frustrating workflow and it was necessary when you were memory limited on older console generations. Luckily we have large memory budgets these days and dont need to resort to horrible things like this.
All these things are covered in the Riot/BitSquid and Nicholas’ blog posts. I’m not going to go into too much more detail. What I’ll discuss now is what I’ve decided to do in terms of track compression…
I’ve decided not to compress tracks…

Hold on… hear me out…
While I do keep the data in terms of tracks, I keep all rotation data for all frames. When it comes to translation and scale I track whether the translation and scale is static at compression time and if it is I only store the single value per track. So if a track translates on X but not Y and Z, I will store all the values for the translation X track but only a single value for the translation Y and Z tracks.
This is true for most of our bones in around 95% of our animations, so we can end up with massive reductions in memory with absolutely no addition loss in quality. This does require some work on the DCC side to ensure that we dont end up with minor translations and scales on bones as part of the animation workflow but that’s a one time tooling investment cost.
For an example animation, we only have two tracks with translation and no tracks with scale. The amount of data we need for 1 second of animation now becomes: 18.6KB down from 41KB (and around 20% of the original data). And it gets even better, if the length of the animation increases, we only pay for the rotation and dynamic translation tracks while the cost for the static tracks stay constant which will result in bigger relative savings for longer animations. And we have no additional loss in quality over that incurred by the quantization.
So given all that information my final data layout looks like this:
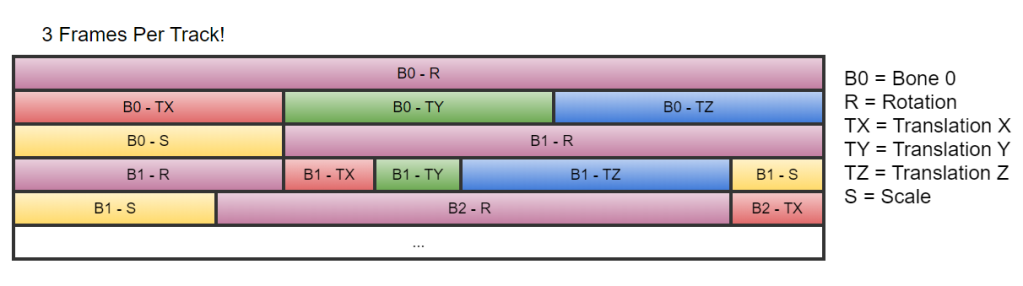
I also keep the offset into the data block for the start of each bone’s data. This is needed since sometimes we need to sample just the data for a given bone without reading a full pose. This allows us a fast way to access the track data directly.
In addition to the animation data which is stored in a single block of memory, I also have compression settings per track:

These settings contain all the data I need to decode the quantized values per track. It also tracks which of the tracks are static if any so that I know how to deal with the compressed data when I hit that track during sampling.
You’ll also noticed quantization ranges per track, when I compressed I track the min and max values for each feature (e.g. translation in X) per track and so ensure that I quantize the data to the min/max range per track so as to try to keep as much precision as possible. I don’t think it’s really possible to have global quantization ranges that dont either break your data (once values are outside the range) or introduce significant errors.
Anyways that was a quick brain dump of an idiot trying to do animation compression with the end result being I don’t do much compression 🙂